Сумма внутренних углов пятиугольника является важной характеристикой этой геометрической фигуры. Рассмотрим подробно, как вычисляется этот показатель и какие закономерности ему соответствуют.
Содержание
Формула для вычисления суммы углов
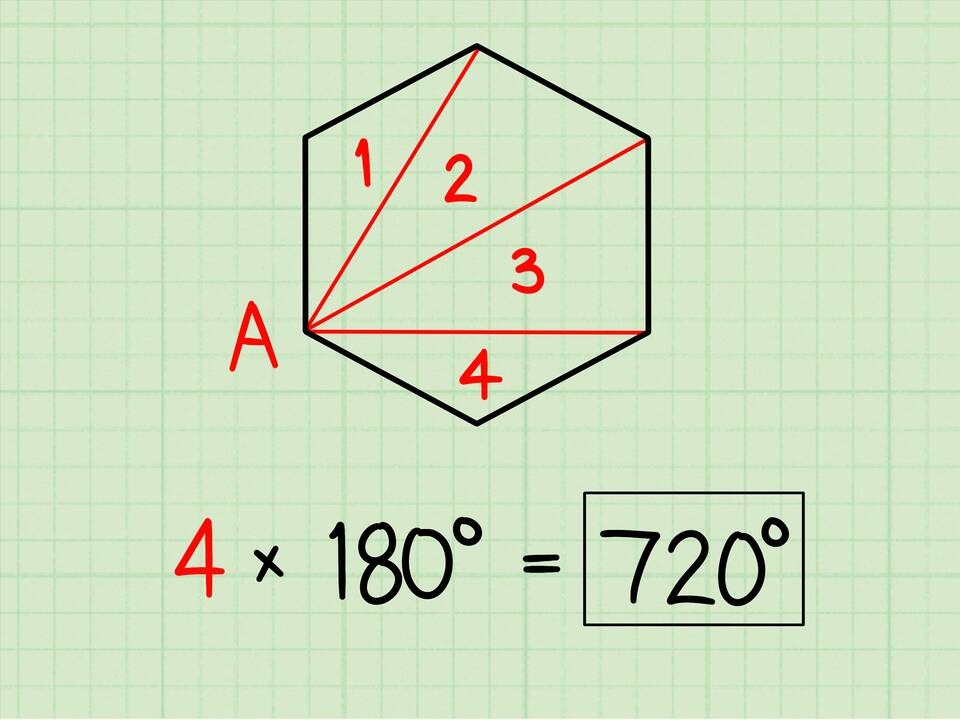
Для любого выпуклого n-угольника сумма внутренних углов вычисляется по формуле:
| Формула | S = (n - 2) × 180° |
| Для пятиугольника (n=5) | S = (5 - 2) × 180° = 540° |
Доказательство формулы
Метод разбиения на треугольники
- Из одной вершины проводим все возможные диагонали
- Пятиугольник разбивается на 3 треугольника (5-2=3)
- Сумма углов каждого треугольника равна 180°
- Общая сумма: 3 × 180° = 540°
Альтернативные методы расчета
- Использование внешних углов
- Применение векторного анализа
- Графический метод измерения
Свойства углов пятиугольника
| Тип пятиугольника | Особенности углов |
| Правильный пятиугольник | Все углы равны 108° (540° ÷ 5) |
| Неправильный выпуклый | Сумма 540°, углы различны |
| Вогнутый пятиугольник | Один угол больше 180°, но сумма та же |
Практическое применение
- Архитектура и строительство
- Дизайн и декоративное искусство
- Компьютерная графика
- Геодезические расчеты
Интересные факты
- В природе пятиугольные структуры встречаются у некоторых морских организмов
- Пентагон (здание) имеет форму правильного пятиугольника
- Звездчатые пятиугольники имеют другие угловые характеристики
Заключение
Сумма внутренних углов пятиугольника всегда равна 540° для любого простого выпуклого пятиугольника. Это знание является фундаментальным в геометрии и находит применение во многих практических областях. Для правильного пятиугольника каждый угол составляет 108°, что создает уникальные геометрические свойства этой фигуры.